Quantum Computing Poses Remote Risks

Key takeaways

The theoretical advantage of quantum computing remains elusive and is unlikely to cause a disruption in the next decade.

If achieved, quantum advantage poses serious threats to cryptocurrencies like Bitcoin, which utilize elliptic curve encryption and proof of work consensus.

Bitcoin and other cryptocurrencies are technological solutions, at risk of becoming obsolete and losing value if they fail to adapt in a rapidly advancing technological world.

Introduction

Research and development in quantum computing has been gaining momentum and attention over the past few years. However, the technology is not entirely new. It is based on a theory that was established in the early 1980’s with contributions from famous scientists like Paul Benioff and Richard Feynman[1]. Promising quantum algorithms for integer factoring(Shor [2]) and unstructured searches(Grover [3]) were discovered in the 1990’s, predating the Bitcoin whitepaper of 2009 [4].

In 2023, IBM released an optimistic report suggesting that a race to quantum advantage is underway[1]. The report defines quantum advantage as the state in which a computing task of practical interest can be performed “more efficiently, more cost effectively, or with better quality” using quantum computers. It outlines many potential application areas for quantum computing: healthcare, insurance, finance and banking, chemicals and petroleum, electronics, logistics, and other areas. However, the report fails to discuss potential applications to cryptocurrencies. Fortunately, a 2022 article, Quantum advantage on proof of work [5], describes potential impacts on Bitcoin’s consensus protocol. Last month, Ledger posted a blog discussing the threat quantum computing poses to cryptocurrencies through breaking encryption.

The objective of this post is to continue discussions from some of the mentioned publications and create awareness about quantum computing, its advancement, and potential impact on Bitcoin and other cryptocurrencies.  

Overview of Quantum Computing

Quantum computing is a general categorization that can be defined from DiVincenzo's five criteria:

1.      A scalable physical system with well-characterized qubit

2.      The ability to initialize the state of the qubits to a simple fiducial state

3.      Long relevant decoherence times

4.      A "universal" set of quantum gates

5.      A qubit-specific measurement capability

Quantum computing is different from the deterministic nature of classical computing. It is more of a probability boosting tool that helps narrow in on a desired solution as opposed to randomly trying to find it by trial and error. To use a familiar analogy, quantum computers share some similarities with rolling dice. Suppose you had special dice that you could roll to find an answer to a question by trial and error where the probability of the dice giving the right answer can be increased by rolling them in a certain way. This is similar to how a quantum computer works. The dice in a quantum computer are its quantum bits or qubits. When they are rolling, they are in superposition. The shaking of the dice in a coordinated manner such that they are predictably dependent on each other is entanglement. The ability to roll them so that the likelihood of certain combinations are greatly reduced, and consequently others are more likely, is interference. Obviously, dice are not qubits, but qubits can take multiple forms: trapped ions, superconducting, neutral atoms, photonic fusion-based. Each of these forms have merit in relation to addressing challenges like operation speed, coherence time, gate error rates and others. 

As quantum computing is very different from classical computing, it has certain advantages and disadvantages. Where a classical bit only exists in the computation states of zero and one, qubits exist in superposition, an infinite number of states simultaneously. Superposition is represented by a phase with the probability of being measured as either zero or one. It should be noted that qubits cannot be measured in quantum states other than zero or one; measurement causes decoherence from the superposition state. The computational advantages stem from superposition, entanglement and interference. These properties enable running theoretical quantum algorithms to efficiently solve problems, which are inefficient or infeasible to solve classically. Difficulty in proof of work(POW) mining or finding a private key for a certain public key in elliptic curve cryptography(ECC) have the potential to be solved efficiently with qubits. 

However, the useful state of qubits is coupled with the disadvantages of instability and fragility. To achieve computational advantage operations must be executed on qubits while entangled in superposition under a preserved quantum state. However, qubits experience decay in superposition and disruptions of phase coherence, quantified as median times, T1 and T2, respectively. Disturbances due to random external factors are next to impossible to eliminate entirely and phase coherence cannot exist when superposition decays. Therefore, qubits are limited by their coherence time T2, which also represents the period in which operations of logical circuits for algorithms must be executed. The coherence time divided by the two-qubit gate duration represents the maximum number of operations that can be run in series to execute an algorithm. Different qubits have different coherence times and gate durations leading to different performance trade-offs. Documentation from October 2023 tabulates[6] that ion qubits have T2 1000ms and gate duration 0.6ms permitting 1667 operations, superconducting qubits have T2 30 microseconds and gate duration 12 nanoseconds permitting 2500 operations, and neutral atoms have T2 1500ms and gate duration 0.25ms permitting 6000 operations. We can see that superconducting qubits are faster while neutral atoms allow for larger circuits. 

Moreover, carrying out operations on the qubits in superposition precludes step-by-step verification and error correction, as they are only measurable in their computational states of zero or one and the state of qubits can not be cloned. Consequently, operational errors tend to accumulate over a series of operations. This leads to noisy results characterized by a low probability of being correct, referred to as low fidelity. There are approaches to fault tolerant quantum computing(FTQC), involving using many physical qubits to construct one logical qubit assuming the physical qubits’ error rates do not exceed a certain threshold. The logical qubit serves as one ideal error free qubit in a quantum algorithm. There are significant challenges in maintaining a large number of physical qubits in a useful state. FTQC will be necessary to realize quantum advantage using Shor’s or Grover’s algorithm. However, quantum computing is in the pre-fault tolerant era with FTQC in experimental stages. Furthermore, in the case of Grover’s, some researchers assert that achieving quantum advantage is “unrealistic even under extremely optimistic assumptions on both hardware quality and availability”[15].

IBM measures the computational power of a quantum computer with a metric called Quantum Volume[1] that it developed in 2019. It recognizes that there are many factors that contribute to the effectiveness of a quantum processor. Despite this recognition, companies often are misleading when they promote quantum computing. They focus on qubit count while downplaying coherence time and error rates. Coherence time is an important specification. The gate operations in an algorithm’s logical circuits can only be executed while the qubits are coherent in superposition. The coherence time of the qubits divided by the gate duration determines the depth of the algorithm that can be executed on the processor. Moreover, gate errors compound when applied over large numbers of qubits. Recent estimates[7] indicate that a circuit 100 qubits by 100 gates deep with an error rate of 0.1%, is estimated to have state fidelity of less than 0.0005, representing a low probability of producing a correct result. It is hard to say how much additional performance you will get from a large qubit processor if you do not know the coherence time, gate duration and gate error rate, in addition to other specifications.

To provide an idea of what is currently possible, quantum researchers[7] reported a breakthrough in utility with moderate success for a circuit on 127 qubits with depth of 60. This was achieved through noise mitigation, essentially predicting the amount of error in the result and adjusting for it. Moreover, these results were accomplished on circuits that were designed to demonstrate quantum advantage over classical computing and were not designed to solve any real world problem. It is quite far from fault tolerant quantum computing for thousands of logical qubits running algorithms with depths in the tens of millions needed to realize quantum advantage in POW mining or ECC decryption as has been determined[8]. It should be noted that the quantum advantage demonstrated in the report was later disproved by researchers in 2024 who bettered the quantum computer’s performance classically[9].  

Despite the current nascent stage of quantum computing, research, funding and enthusiasm is abundant from companies, investors, and scientists. It is likely that we will see a great deal of research and development in the coming decade. However, the problems are complicated. Much of the advancement needs to come in the form of hardware and scientific discovery. In general, this can be unpredictable. With promising quantum search and factoring algorithms discovered over twenty-five years ago, one would figure that quantum computers would offer much more utility today if the advancement could have been effectively accelerated. It raises the question:“What should concern us?” Incremental advances involving Grover’s and Shor’s algorithms will be documented and published demonstrating larger successful queries and integers factored. This sort of documentation along with advances in FTQC will provide evidence that a disruption could be on the horizon. However, the potential impacts of quantum computing on encryption and other critical applications have resulted in some secrecy in its development. There is a possibility that a material breakthrough nearing quantum advantage in ECC would not be publicized in the interest of national security, similar to documented attempts to suppress publication of the first encryption algorithms. However, given the limited capabilities of quantum computing evident in published research, even if state entities have some advantage, it does not suggest a risk of disruption is imminent in the next decade[14]. 

Quantum Computing and cryptocurrencies

Bitcoin is the largest cryptocurrency by market cap at $1.1 trillion, over twice the next largest Ethereum at $0.4 trillion, as of February 2024. Bitcoin utilizes a POW consensus protocol and ECC encryption using peer-to-peer key hash(P2PKH) and peer-to-peer script hash(P2PSH). Quantum advantage has the potential to disrupt POW consensus and ECC digital signature applications if technology advances adequately.

Although Ethereum changed its consensus protocol to proof of stake (POS), Bitcoin has retained POW with many conservative members in the Bitcoin community motivated by its purity, remaining true to the original Bitcoin whitepaper and its mysterious elusive author Satoshi Nakamoto. It is very unlikely that Bitcoin will ever change its protocol to POS or any other alternative given the inertia in the community. 

POW involves solving a difficulty problem of finding a number (nonce) from a large set of possibilities such that the SHA256 hash of the nonce with the block data and prior header information is less than a certain number, the largest hash value minus the difficulty value, as expressed below.

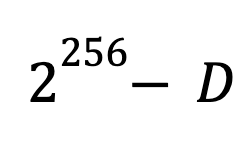
The miner can add a block to the chain that includes their reward if their block solves this difficulty problem. The difficulty adjusts so that given the hash rate of the network, a solution is found at an average rate of one every ten minutes. On average, one nonce is a solution out of the number of hashes made in ten minutes. Classically, the number of independently chosen hashes required to find a solution is expressed by the fraction below.

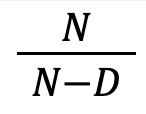
An ideal quantum computer with sufficient coherence time could find a solution using Grover’s algorithm in the number of hashes expressed by the equation below.

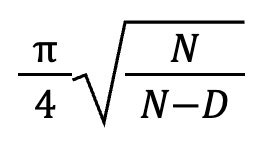
This results in many fewer hashes when the fraction under the square root sign is large.

For example, if the fraction is 1,000,000, classically your solution is expected to require 1,000,000 hashes, but you only need to do about 750 hashes with Grover’s. Assuming operation speed is comparable there would be a tremendous speed advantage using a quantum computer in mining if the technology would permit Grover’s to be run on the large numbers required. 

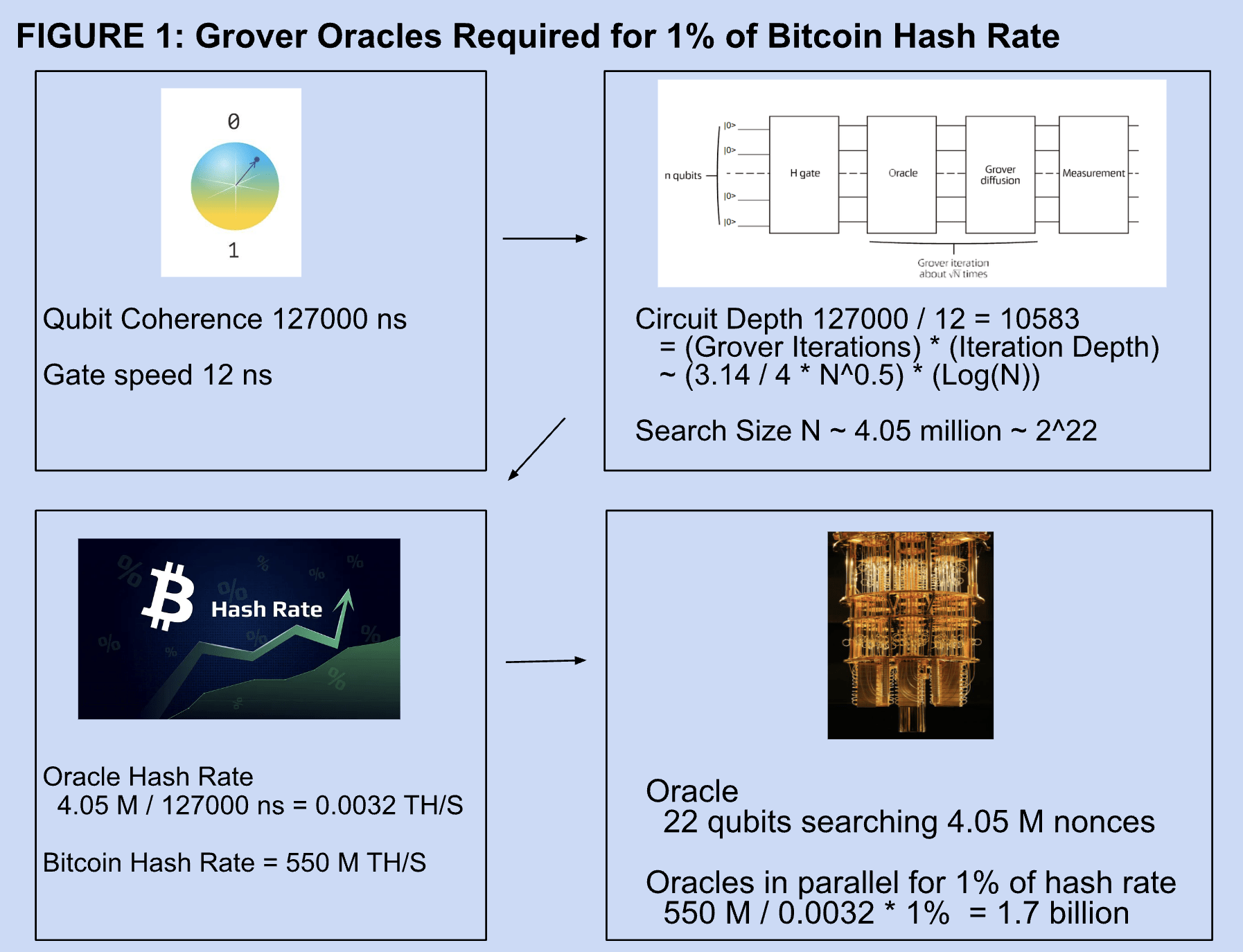
The back-of-envelope estimate of Figure 1 suggests that it would take over 1 billion 22 qubit Grover oracles running in parallel to achieve 1% of the current hash rate of the bitcoin network[11]. Moreover, the gate depth would be over 10,000, which currently would create unmanageable noise in the results. A 2022 article[10] claimed to have performed the largest Grover search to date using six qubits. Six qubits are limited to searches of size 64, suggesting quantum computing will not disrupt mining in the near future.

Bitcoin uses elliptic curve digital signature application (ECDSA) of size 256 bits with P2PSH and P2PKH for encryption of addresses. Basically, the public key is not revealed when receiving BTC, but the public key of the address is revealed when sending. For this reason, BTC addresses are generally only used once in most cases. However, legacy addresses do have public keys revealed, this includes a large number of Satoshi’s addresses. There are no efficient quantum algorithms to inverse a SHA256 hash, thus addresses are safe from any quantum attack in unrevealed form. However, once the public key is revealed, Shor’s algorithm adapted for ECDSA could be run on an ideal quantum computer to find the public key in polynomial time. Classically, finding a solution would be super-polynomial, orders of magnitude slower. Super-polynomial time is infeasible making ECDSA secure under classical computing limitations. Polynomial time is potentially feasible and it is conjectured that eventually, ECDSA will be breakable by quantum computers. However, the number of logical qubits required would be approximately 2330 and with a Toffoli gate depth of over 100 billion[7]. Of course, this is far from possible given the current state of the art in quantum computing.

Potential threats

Achieving quantum advantage in unstructured searches using Grover’s algorithm will likely impact crypto mining[5]. However, prior to mining applications, Grover’s algorithm will likely be applied on a smaller scale to demonstrate advantage over classical searches in applications unrelated to mining. This will likely serve as a precursor to miners experimenting with quantum mining on a small scale. The first quantum mining applications will likely partition the nonce range, running Grover’s algorithm in parallel to reduce the size of the searches. A process has been described[5] in which mining difficulty increases adequately to maintain 10 minute block times, as quantum mining increases hash rates. The introduction of quantum computing to mining could be a gradual process without any acute disruptions to the network. 

However, quantum advantage in mining could lead to more centralization. Initially, cost and availability will make quantum computers limited to few miners. Centralizing forces could persist due to the quadratic advantage using Grover’s algorithm. Quantum search algorithms are most effective when they are run holistically. If you partition a search and run Grover’s in parallel you lose some of its quadratic advantage, as it comes from the square root of the set size being smaller than the set size.

Suppose a set of size N is partitioned into x sets of, each having the size below.

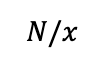
The number of operations for searching the large set is of the order expressed below.

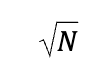
This is less than the order of the number of operations for the partitioned set shown below.

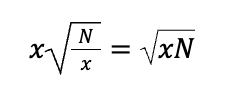
For example, if a quantum miner increased its gate speed by a factor of 2 allowing it to run circuits twice as deep as before the increase, then a mining farm without the speed increase would need to multiply its number of miners by a factor of 4 to keep up with the increased hash rate, see Figure 2. A large quantum computer’s capability exceeds the sum of its parts making it less effective for a distributed network. Technological superiority of one miner cannot be mitigated easily by adding inferior miners in parallel, reducing the competitiveness of decentralization. 

Alternative scenarios to a gradual application of quantum computing are possible. One could imagine an entity acquiring a significant quantum advantage and not apply it to mining until they want to engage in a 51% attack on the network. A state actor could be such an entity, developing quantum computing for other problems and using their advantage in mining if extenuating circumstances require it. For example, a sanctioned entity attempts to transfer a large value of Bitcoin and the National Security Agency(NSA) decides to block the transfer by eliminating it from blocks that it produces to gain control by establishing the largest chain.

The path to quantum advantage using Shor’s algorithm is similar to Grover’s. As quantum computing technology advances, academic papers will indicate that larger integers can be factored effectively with quantum computers. This will likely result in upgrading the encryption for Bitcoin. However, abandoned wallets with lost keys and exposed public keys will be harvested by quantum hackers, as they will have ample time to decrypt the private keys. We would likely see these funds move as the first evidence of quantum decryption of private keys. This may include a large number of Satoshi’s bitcoin. It is estimated that there are at least 34,000 public addresses with 50 BTC each belonging to Satoshi[12]. It is possible that if the NSA had this capability, they would transfer all the bitcoin from these exposed addresses and hold it in their custody for someone to make a claim while simultaneously alerting the relevant tax authorities. The first quantum computer capable of breaking ECDS and draining addresses with exposed public keys could be developed for other applications. State actors or other very large entities with broad objectives are likely candidates for developing powerful quantum computers for general purposes. .

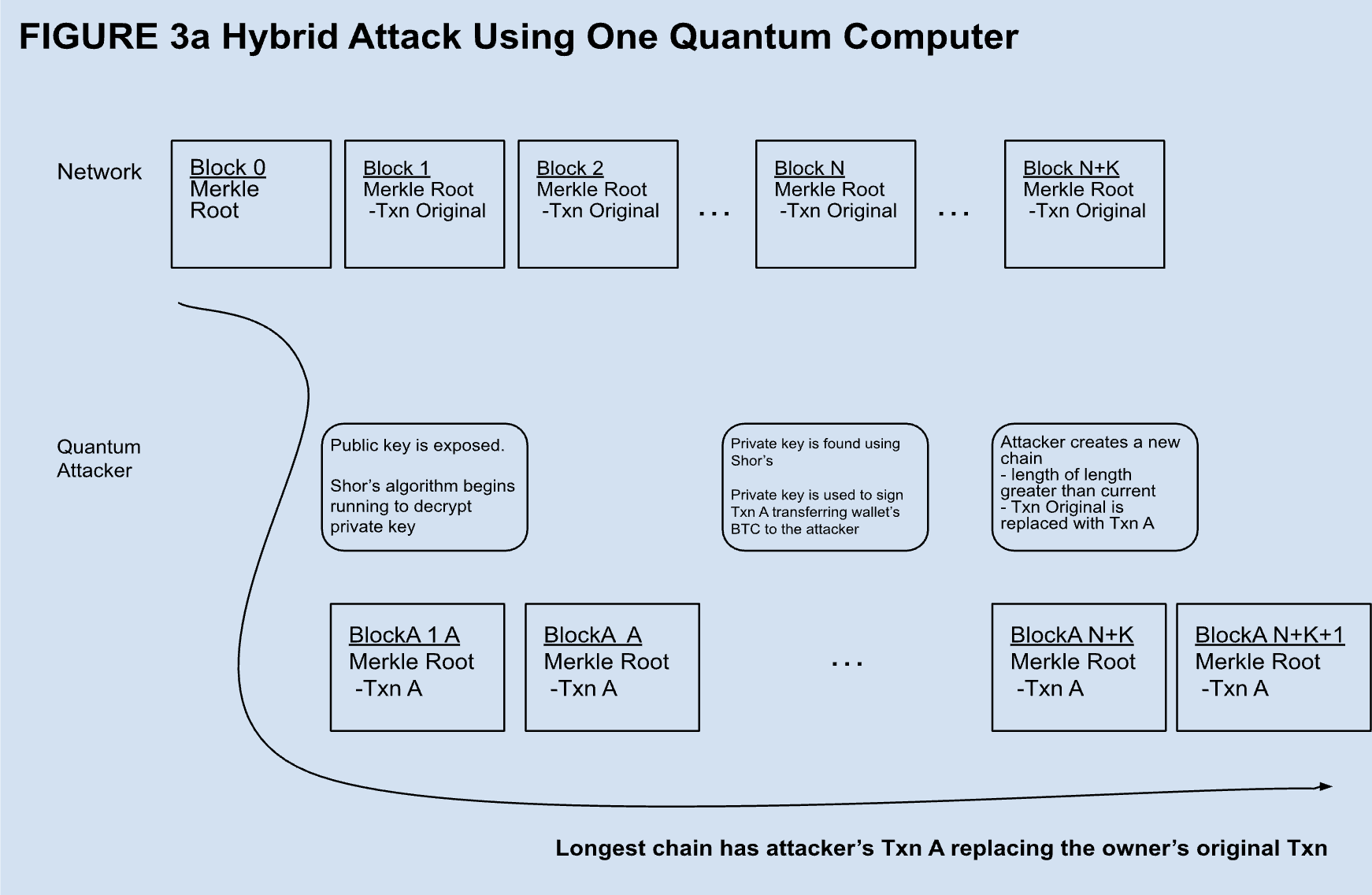
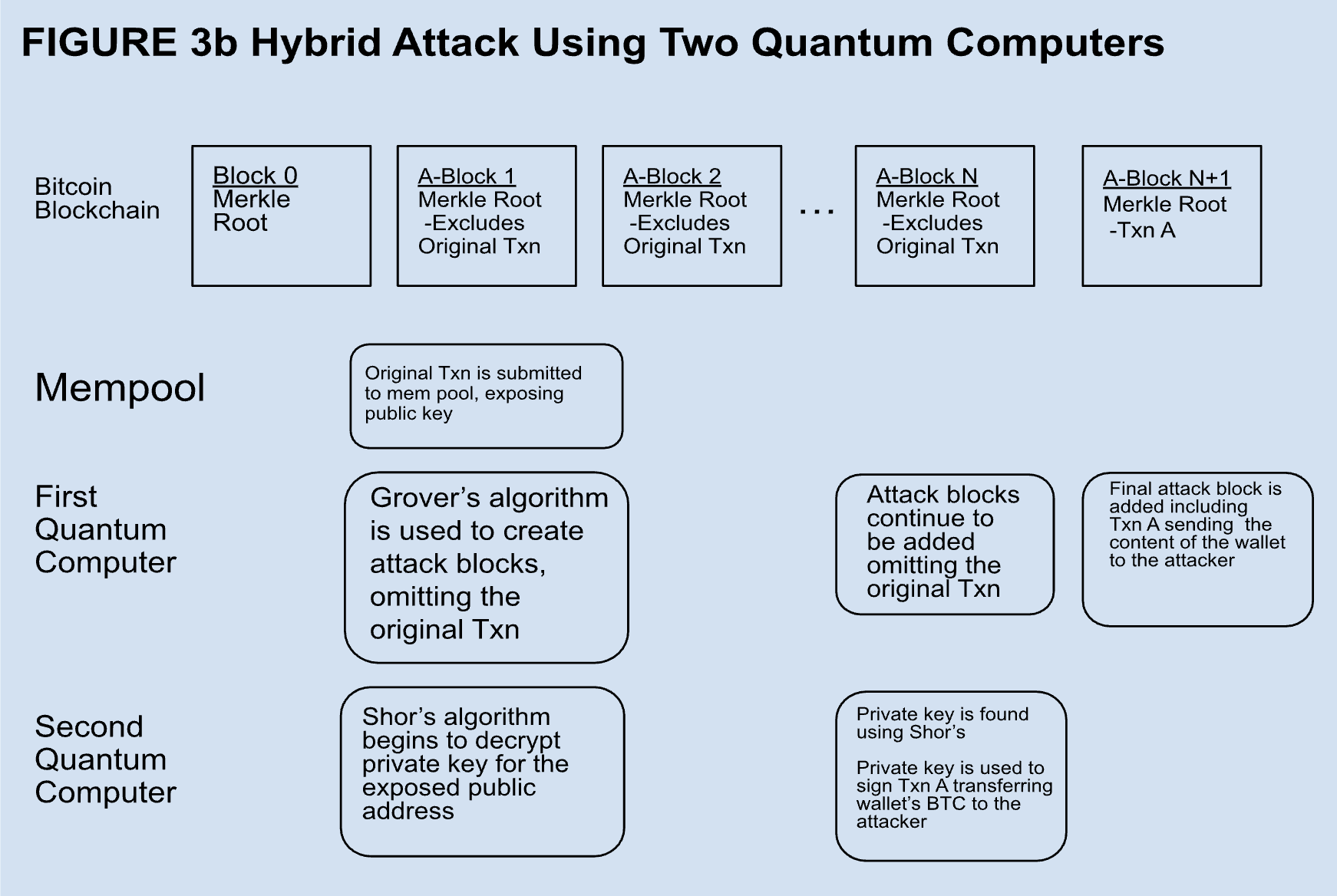
A hybrid attack could be very disruptive, but it is less plausible than others. Essentially, it requires an entity to secretly develop superior quantum capabilities and decide to use them suddenly to steal bitcoin. The way it would work for an attacker with one quantum computer is shown in Figure 3a. In this case, the attacker waits for someone with a P2PKH or P2PSH address to spend bitcoin from a high value wallet. The transaction exposes the public key and is included in a block added within ten minutes. The attacker wants to steal the content of the address so the attacker runs Shor’s algorithm and finds the private key. Then the attacker signs a transaction with the key to send all of the bitcoin that was in the wallet prior to the original transaction to their own address. There may have been a few blocks confirmed already, so the attacker then runs Grover’s algorithm to rapidly create a chain of blocks on top of the one they include their theft transaction in, replacing the block containing the original transaction. The speed of Grover’s allows for a successful 51% attack making their theft transaction part of the longest chain and they have successfully stolen the contents of the address. Theoretically, attacks like this are possible according to the consensus protocol. In reality, it is likely that an attack like this would be detected and there would be some steps taken by the community to protect Bitcoin’s integrity. However, if the quantum attacker had two sufficiently powerful quantum computers, the attack could be far more insidious, as shown in Figure 3b. In this case, one quantum computer could be used to produce blocks omitting the original transaction in the Mempool while the other quantum computer decrypts the exposed public key. Once the private key is found, the theft transaction is included in the next block and the content of the wallet is stolen without the original transaction ever having been included in a block. If attacks like these became prevalent, Bitcoin would no longer be secure and it would cease to be a store of value. Even the staunchest maximalist, adverse on a cellular level to any deviation from the original Satoshi whitepaper, would agree to make the necessary upgrades to save the network.

With the exception of abandoned exposed public addresses, Bitcoin and other non-privacy cryptocurrencies are not very susceptible to the hacking technique of Harvest Now, Decrypt Later. However, privacy coins like Monero propose value in concealing information about transactions. Encrypted information is highly susceptible to this technique of acquiring encrypted information with the intention of decrypting it and gaining information when decryption becomes feasible. Privacy coins will need to be more proactive updating to quantum resistance in order to protect their value. Apple's iMessage has begun to use module lattice encryption to preclude Harvest Now, Decrypt Later quantum attacks[13]. Although the risk may seem remote, it is prudent, as protected information could be relevant decades after encryption. 

Quantum computing is a matter of national security and could be developed in secret. Its current capabilities may be difficult to assess accurately, adding to the risk of an acute disruption. However, it has been argued that quantum advancements will be gradual and available through cloud services[5], giving Bitcoin’s community time to adapt prior to any acute disruption. The risks of quantum computing to Bitcoin and other cryptocurrencies will be influenced by how quantum computing is integrated into the networks. While gradual integration of quantum computing would be preferable and less disruptive than an abrupt one, any successful application of quantum computing to cryptocurrencies will impact networks significantly.

Conclusion

Quantum computing is an exciting technology combining theoretical physics with practical engineering and computation. The race for ever faster and more efficient processors has incentivized its development. Consequently, companies developing quantum processors are promoting quantum advantage while downplaying complexity of unsolved problems that thwart progress towards its achievement. Realizing the theoretical potential of quantum computing remains difficult and slow despite recent efforts. 

As Bitcoin and cryptocurrency stakeholders we must be aware of the advancement of quantum computing because of its potential disruptions, however remote they may be. More generally, we must remain aware of all new technology possessing disruptive potential. Although Bitcoin is founded on principles of sound money, its existence lies in technology. It cannot retain its value by remaining static like gold and other versions of sound money. Bitcoin must evolve to remain current in an advancing technological world. Otherwise, it will be at risk of becoming obsolete and losing its value. 

References

1. “The Quantum Decade”, Fourth Edition, IBM Institute for Business Value. Accessed January, 2024. https://www.ibm.com/thought-leadership/institute-business-value/en-us/report/quantum-decade

2. Shor, Peter W. (1997), "Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer", SIAM J. Comput., 26 (5): 1484–1509, arXiv:quant-ph/9508027v2, Bibcode:1999SIAMR..41..303S, doi:10.1137/S0036144598347011. Revised version of the original paper by Peter Shor ("28 pages, LaTeX. This is an expanded version of a paper that appeared in the Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, Nov. 20--22, 1994. Minor revisions made January, 1996").

3. Grover L.K.: A fast quantum mechanical algorithm for database search, Proceedings, 28th Annual ACM Symposium on the Theory of Computing, (May 1996) p. 212

4. Satoshi Nakamoto. Bitcoin: A peer-to-peer electronic cash system. http://bitcoin.org/bitcoin. pdf, 2009

5. Dan A. Bard, Joseph J. Kearney, Carlos A. Perez-Delgado, Quantum advantage on proof of work, Array, Volume 15, 2022, 100225, ISSN 2590-0056, https://doi.org/10.1016/j.array.2022.100225. (https://www.sciencedirect.com/science/article/pii/S2590005622000650)

6. Alex Lukin and Tommaso Macri, Guest Post — Unlocking The Quantum Frontier: Coherence In Neutral-Atom Systems, https://thequantuminsider.com/2023/10/03/guest-post-unlocking-the-quantum-frontier-coherence-in-neutral-atom-systems/

7. Youngseok Kim, Andrew Eddins, Sajant Anand, Ken Xuan Wei, Ewout van den Berg, Sami Rosenblatt, Hasan Nayfeh, Yantao Wu, Michael Zaletel, Kristan Temme & Abhinav Kandala, Evidence for the utility of quantum computing before fault tolerance, Nature, June 2023, Evidence for the utility of quantum computing before fault tolerance | Nature

8. Martin Roetteler, Michael Naehrig, Krysta M. Svore, and Kristin Lauter, Quantum Resource Estimates for Computing Elliptic Curve Discrete Logarithms, Microsoft Research, USA, 2017
   https://eprint.iacr.org/2017/598.pdf

9. Tindall, Joseph and Fishman, Matthew and Stoudenmire, E. Miles and Sels, Dries, Efficient Tensor Network Simulation of IBM's Eagle Kicked Ising Experiment, PRX Quantum, vol 5, issue 1,American Physical Society, January 2024 https://link.aps.org/doi/10.1103/PRXQuantum.5.010308

10. Dinesh Reddy Vemula, Debanjan Konar, Sudeep Satheesan, Sri Mounica Kalidasu, Attila Cangi, A Scalable 5,6-Qubit Grover's Quantum Search Algorithm, arXiv:2205.00117 [quant-ph], https://doi.org/10.48550/arXiv.2205.00117

11. February 2024, https://www.blockchain.com/explorer/charts/hash-rate

12. February 2024, https://github.com/Crypt0hunter/Public-keys-for-Satoshi-Nakamoto-wallets?tab=readme-ov-file

13. February 2024, https://security.apple.com/blog/imessage-pq3/

14. Charles Guillemet, Victor Servant, Should Crypto Fear Quantum Computing? | Ledger, February 2024

15. E.M. Stoudenmire, Xavier Waintal, Grover’s Algorithm Offers No Quantum Advantage, arXiv:2303.11317v1, https://doi.org/10.48550/arXiv.2303.11317